Eau de Cologne
Yukicoder No. 93 ペガサス 본문
Yukicoder No. 93 페가수스
문제
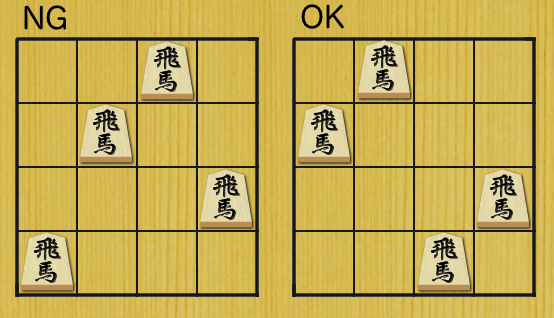
나오키 군은 $N \times N$격자의 $N$개의 "비마"(飛馬)라 불리는 신기한 말을 가지고 있습니다. "비마"는 쇼기의 비차(飛車)와 계마(桂馬)의 움직임을 합친 말입니다. (각주: 비차는 상하좌우로 원하는 만큼 이동할 수 있는 말이며, 계마는 앞으로 두 칸, 왼쪽 혹은 오른쪽으로 한 칸 움직일 수 있는 말입니다.)

어느 날 말을 배치하던 중에, "서로를 잡을 수 없도록 $N$개의 비마를 놓을 수 있는 방법"이 있다는 것을 발견했습니다.
이 조건을 만족하는 배치의 경우의 수를 $10^9+7$로 나눈 나머지를 구하는 프로그램을 작성해주세요.
단, 각 말의 구분은 없고, 모든 말은 위쪽 방향을 가리키고 있습니다.
입력
$N \ (1 \le N \le 1000)$이 주어집니다.
출력
조건을 만족하는 배치의 경우의 수를 $10^9+7$로 나눈 나머지를 출력해주세요.
풀이
힌트
$N \times N$ 격자 배치에 $N+1$행에 새로운 말을 삽입하면 무슨 일이 일어날까요?
풀이
문제를 요약하면, 인접한 두 수의 차가 $2$인 경우가 없는 길이 $N$인 순열의 가짓수를 구하는 문제입니다.
다음과 같은 정의로 동적 계획법 테이블을 정의합시다.
$DP_{i, j, k, s}$
- $i \times i$ 격자에 $i$ 개의 말을 배치합니다.
- 인접한 두 수의 차가 $2$인 위치가 $j$개 있습니다.
- $k$가 참이라면, 수 $i$와 수 $i-2$가 인접하게 존재합니다.
- $s$가 참이라면, 수 $i-1$과 수 $i-3$이 인접하게 존재합니다.
우리는 길이 $i$인 순열에 길이 $i+1$인 순열을 끼워 넣는 경우를 생각해 볼 것입니다. $i+1$이 들어갈 수 있는 위치는 총 $i+1$가지가 존재하며, 각각은 $(i, j, k, s)$상태를 다음과 같이 바꿔놓습니다.
- 인접한 두 수의 차가 $2$인 위치에 들어가는 경우는 $j$가지 있습니다. 이 경우에는, $j$가 $1$ 감소합니다.
- 일반적인 경우에는, 해당 위치는 $(i+1)-2$와 인접하지 않기 때문에, $k$는 거짓, $s$는 기존 $k$의 값이 됩니다.
- 단, $k$가 참일 경우에는 $i$와 $i-2$사이에 끼어 들어가는 경우를 따로 생각해야 합니다.
- 단, $s$가 참일 경우에는 $i-1$과 $i-3$사이에 끼어 들어가는 경우를 따로 생각해야 합니다. 이 경우에, 인접한 위치가 하나 없어지고, 하나 생기기 때문에 $j$는 변하지 않으며, $k$는 참이 됩니다.
- 인접한 두 수의 차가 $2$가 아닌 위치에 들어가는 경우는 $(i+1)-j$가지 있습니다.
- 이 경우, $s$는 항상 기존 $k$의 값이 됩니다.
- 해당 위치가 $i-1$ 옆인 경우는 따로 세 주어야 합니다. 이 경우 $j$는 $1$ 증가하고, $k$는 참이 됩니다.일반적으로는 왼쪽, 오른쪽 두 가지 경우가 있지만, $s$가 참인 경우 위에서 세어 줬습니다.
- 해당 위치가 $i-1$ 옆이 아닌 경우를 세어주면 됩니다.
이렇게 구현을 하면, DP의 상태는 $O(N^2)$개이고, 각각 상수 시간에 계산 가능하기 때문에, 총 $O(N^2)$ 시간에 문제를 해결할 수 있습니다.
'Yukicoder' 카테고리의 다른 글
| Yukicoder No. 114 遠い未来 (0) | 2022.02.03 |
|---|---|
| Yukicoder No. 95 Alice and Graph (0) | 2022.01.31 |
| Yukicoder No. 67, 68 よくある棒を切る問題 (0) | 2022.01.25 |
| Yukicoder No. 54 Happy Hallowe'en (0) | 2022.01.24 |
| Yukicoder No. 31 悪のミックスジュース (0) | 2022.01.23 |
